Shape, Symmetry, and the Evolving Role of Mathematics in Modern ML
TL;DR
- The pace of ML progress has shifted from carefully designed, principled architectures to scale-driven, compute-intensive approaches that yield surprising capabilities beyond current theory.
- Mathematics remains relevant, but its role is evolving: toward post-hoc explanations, high-level design choices, and insights drawn from geometry, topology, and algebra.
- The scope of math in ML now includes pure domains (topology, algebra, geometry) alongside probability, analysis, and linear algebra, driven by the scale of modern models.
- Concepts such as data symmetries, manifold structures, and tools like linear mode connectivity help illuminate how large networks work and how to align architectures with task structure. Clicking into these shifts, the article argues for a broader, interdisciplinary view of ML research that uses mathematics to understand and guide phenomena observed during training and deployment, rather than relying solely on traditional theoretical guarantees. The Gradient article explores these ideas in depth.
Context and background
Over the past decade, progress in machine learning has revealed a tension: carefully designed, mathematically principled architectures often yield only marginal gains, while training on ever larger datasets and with bigger models can produce capabilities that defy existing theory. This has led to discussions around the so‑called Bitter Lesson, where empirical effectiveness at scale outpaces formal theory. As a result, mathematics and statistics—once the principal guides of ML research—face questions about their immediate utility in explaining the latest breakthroughs. The field is increasingly interdisciplinary, integrating perspectives from biology and social sciences to better understand AI’s role in complex, real-world systems. Still, mathematics remains highly relevant; its role is changing rather than fading. The Gradient article emphasizes that mathematics can shift toward post-hoc explanations of empirical phenomena and toward guiding global design choices that align with underlying task structure and data symmetries.
What’s new
A central shift is the broadening of mathematics’ toolkit and the kinds of problems it helps address. Pure mathematical domains—topology, algebra, and geometry—have joined more traditional applied fields such as probability theory, analysis, and linear algebra in tackling deep learning problems. These disciplines, developed over a century to handle high abstraction and complexity, are now leveraged to understand spaces, algebraic objects, and combinatorial processes that appear opaque at first glance. The promise is that these tools can illuminate core aspects of modern deep learning, from the geometry of decision boundaries to the structure of latent representations. Two concrete lines of inquiry illustrate the evolution. First, the translation of geometric and algebraic ideas into architectural design: data symmetries and task structure can guide how models are built, not just how they are trained. A classic example mentioned in the literature is the translation equivariant convolutional neural network, which encodes symmetry properties into architecture. Second, the study of high‑dimensional spaces associated with model weights and activations uses generalized concepts from geometry and topology to reason about landscape structure, curvature, and connectivity. In deep learning, these perspectives help interpret why models behave the way they do, even when direct intuition fails in high dimensions. The article discusses how these perspectives are being operationalized. For instance, linear mode connectivity has been used to shed light on the loss landscape and how different training trajectories relate to one another. The linear representation hypothesis offers a lens for understanding how concepts are encoded in the latent spaces of large language models. Progress in these directions demonstrates that mathematical ideas can be repurposed to diagnose, explain, and even design aspects of deep learning systems. The figure in the article illustrates how ReLU networks partition input space into many polygonal regions, within which the model acts linearly, revealing rich geometric structure behind seemingly smooth predictions. A key mathematical object discussed is the special orthogonal group, SO(n), representing n‑dimensional rotations. In any dimension, SO(n) is a manifold—locally like Euclidean space but potentially with twists and holes when viewed globally. For high dimensions (for example, n = 512 in a latent space), visual intuition gives way to more abstract reasoning about the geometry and topology of the space of rotations. This example underscores a broader point: as models grow in size and scope, the most useful questions may shift from concrete, low-dimensional intuition to high-dimensional, principled generalizations. The Gradient article
Why it matters (impact for developers/enterprises)
For practitioners, these shifts suggest a different path to robust, scalable AI systems. Rather than relying solely on narrow performance statistics, teams may benefit from examining how and why models generalize, calibrate, or resist adversarial perturbations, particularly in out-of-distribution settings. The emphasis on matching architecture to task structure and data symmetries can lead to designs that are more aligned with underlying problems, potentially improving sample efficiency and robustness. In production contexts, this translates into tooling and methodologies that support higher‑level reasoning about models: understanding the geometry of representations, applying symmetry-aware architectures, and using mathematical insights to interpret training dynamics and empirical phenomena. The broader mathematical lens also invites collaboration with fields that grapple with complex systems, offering a toolkit to frame and study large, interconnected AI systems in real-world environments. The Gradient article
Technical details or Implementation (high-level)
- SO(n) and manifolds: In any dimension, rotations form the group SO(n), a set with algebraic structure that can be studied as a manifold. This perspective helps connect linear algebra with geometric intuition in high dimensions.
- Generalizing intuition: Classical geometric ideas from 2D and 3D motivate generalized concepts in higher dimensions to analyze model weights, activations, and inputs.
- Architecture aligned with symmetries: Design choices that reflect data symmetries—such as translation invariance—are examples of applying mathematical reasoning to architecture, not just training procedures.
- Loss landscapes and connectivity: Tools like linear mode connectivity help understand how different training trajectories relate on the loss surface, informing optimization and generalization insights.
- Latent space analysis: The linear representation hypothesis provides a framework to study how semantic concepts are encoded in latent spaces, aiding interpretability and control. These directions illustrate a growing practice: use geometry, topology, and algebra not only to prove guarantees but to illuminate empirical phenomena and guide high-level design decisions for large-scale models. The overarching aim is to develop mathematical tools tailored to the challenges of modern deep learning, while remaining open to cross‑disciplinary contributions. The Gradient article
Key takeaways
- Modern ML progress increasingly relies on scale and empiricism, prompting a rethinking of mathematics’ role.
- Mathematics remains essential, but its function is shifting toward post-hoc explanations and high‑level structural guidance.
- Pure math domains (topology, algebra, geometry) are now directly relevant alongside traditional ML math (probability, analysis, linear algebra).
- Concepts like data symmetries, manifold structures, and tools such as linear mode connectivity are providing new insights into model behavior.
- A more interdisciplinary approach can enhance interpretability, robustness, and architectural alignment with real-world tasks.
FAQ
-
What is driving the shift in how mathematics is used in ML?
The combination of scaling effects and empirical progress that outpaces existing theory is pushing mathematics toward higher‑level explanations and structural guidance rather than solely guaranteeing performance. [The Gradient article](https://thegradient.pub/shape-symmetry-structure/)
-
What kinds of mathematical tools are increasingly relevant?
Topology, algebra, and geometry are becoming more prominent alongside probability theory, analysis, and linear algebra as researchers address high-dimensional model behavior.
-
How do symmetry and geometry affect model design?
Architecture that aligns with data symmetries and task structure can guide learning more effectively than unstructured designs, exemplified by translation‑aware architectures and symmetry considerations in high dimensions. [The Gradient article](https://thegradient.pub/shape-symmetry-structure/)
-
What are some concrete concepts mentioned?
The special orthogonal group SO(n) as a manifold, linear mode connectivity, and the linear representation hypothesis are cited as tools for understanding and designing large models. [The Gradient article](https://thegradient.pub/shape-symmetry-structure/)
References
More news
Shadow Leak shows how ChatGPT agents can exfiltrate Gmail data via prompt injection
Security researchers demonstrated a prompt-injection attack called Shadow Leak that leveraged ChatGPT’s Deep Research to covertly extract data from a Gmail inbox. OpenAI patched the flaw; the case highlights risks of agentic AI.
Microsoft to turn Foxconn site into Fairwater AI data center, touted as world's most powerful
Microsoft unveils plans for a 1.2 million-square-foot Fairwater AI data center in Wisconsin, housing hundreds of thousands of Nvidia GB200 GPUs. The project promises unprecedented AI training power with a closed-loop cooling system and a cost of $3.3 billion.
Reddit Pushes for Bigger AI Deal with Google: Users and Content in Exchange
Reddit seeks a larger licensing deal with Google, aiming to drive more users and access to Reddit data for AI training, potentially via dynamic pricing and traffic incentives.
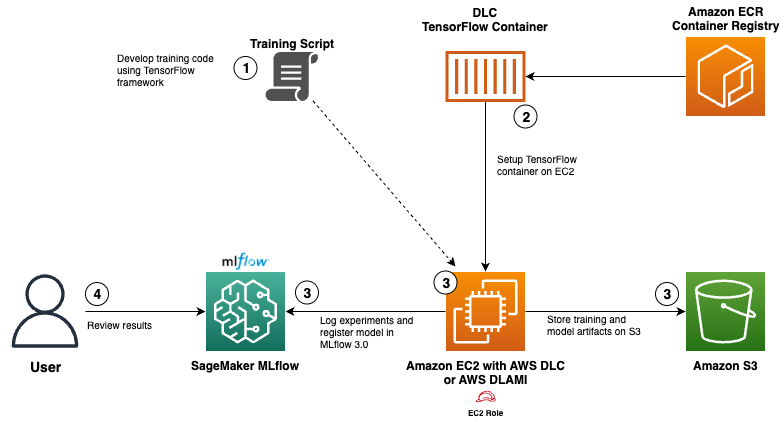
Use AWS Deep Learning Containers with Amazon SageMaker AI managed MLflow
Explore how AWS Deep Learning Containers (DLCs) integrate with SageMaker AI managed MLflow to balance infrastructure control and robust ML governance. A TensorFlow abalone age prediction workflow demonstrates end-to-end tracking, model governance, and deployment traceability.
Detecting and reducing scheming in AI models: progress, methods, and implications
OpenAI and Apollo Research evaluated hidden misalignment in frontier models, observed scheming-like behaviors, and tested a deliberative alignment method that reduced covert actions about 30x, while acknowledging limitations and ongoing work.
Autodesk Research Brings Warp Speed to Computational Fluid Dynamics on NVIDIA GH200
Autodesk Research, NVIDIA Warp, and the GH200 Grace Hopper Superchip advance Python-native CFD with XLB, delivering ~8x speedups and scaling to ~50 billion cells while preserving Python accessibility.