Neural algorithmic reasoning: aligning GNNs with classical algorithms for reliable generalisation
Sources: https://thegradient.pub/neural-algorithmic-reasoning
TL;DR
- Graph neural networks (GNNs) can align with classical dynamic programming algorithms like Bellman-Ford to learn to execute computations.
- Algorithmic alignment improves sample efficiency and generalisation, but is not a universal fix; models can still overfit to training distributions and struggle out-of-distribution.
- The approach has yielded specialized GNNs for linearithmic sequence algorithms, iterative algorithms, pointer-based data structures, and persistent memory, with further links to linear algorithmic alignment and broader theoretical insights.
- Reliability, compositionality and out-of-distribution generalisation are central goals for AI systems, guiding the development of neural models that reason more like classical computation.
Context and background
The article begins from the realm of classical computation—the kind taught in algorithms and data structures courses, including problems like shortest paths, sorting, problem decomposition, and efficient data organization. The author connects this tradition to modern neural networks, asking how neural models might capture such computation. A personal throughline is competitive programming, which motivated the author to study these ideas and to pursue a career in machine learning. A key motivation is that classical algorithms exhibit desirable properties that many deep neural networks struggle with: reliability, generalisation to novel inputs, and interpretability. The author notes that neural networks often lack guaranteed accuracy, fail on out-of-distribution inputs, and behave as black boxes with compounding errors that hinder compositionality. These are precisely the kinds of issues that hinder AI systems from being instructive and useful to humans. The hope is that by capturing traits of classical computation in deep neural networks, AI systems can become more reliable and broadly applicable. The foundational question behind this line of work asks whether neural networks can learn to execute classical algorithms—a benchmark of algorithmic competence that can illuminate how “algorithmic” a model truly is. A landmark MIT study, summarized in The Gradient’s discussion, established a mathematical foundation for why certain architectures might be better for algorithmic tasks: better algorithmic alignment can lead to better generalisation. The study uses Bellman-Ford, a dynamic programming algorithm for shortest-path estimation, as a concrete example where a graph neural network’s data-flow can mirror the algorithm’s structure. This alignment—where neural architectures decompose tasks in a way that mirrors the target algorithm—forms the intuition behind algorithmic alignment. The broader claim is that dynamic programming, and DP-style computation in particular, provides a versatile lens through which many classical computations can be expressed and learned by neural models. This line of work highlights a crucial insight: algorithmic alignment is valuable, but it does not magically solve every challenge. A well-aligned model may still overfit if its inductive biases are not used carefully, especially when facing distributions that differ from the training data. The work argues for deliberate architectural choices and training strategies that respect the structure of the target algorithms. The authors’ own empirical program adds a rigorous evaluation of learning-to-execute with GNNs, alongside prior theoretical and empirical findings.
What’s new
The authors describe their own contributions to the field as part of a broader effort to understand learning-to-execute with GNNs. In their NEGA paper, released concurrently with Xu et al., they present a thorough empirical analysis of learning-to-execute with graph neural networks. The central takeaway is nuanced: while algorithmic alignment is a powerful tool for model class selection, it does not justify reckless application of any expressive GNN to an algorithmic task. Overfitting to training distributions remains a risk, and true execution requires careful inductive biases. From their experiments, three key observations emerge about inductive biases: using these biases strengthens algorithmic alignment for path-finding problems and enables generalisation to inputs up to five times larger at test time. While the article does not enumerate every bias in one place, it emphasizes that these biases push GNNs toward following the target algorithm’s structure rather than exploiting superficial cues in the data. This perspective aligns with broader research on making neural models more faithful to algorithmic procedures and more robust to distribution shifts. The authors also connect their findings to a lineage of algorithmic-alignment work. The idea of aligning neural computation with algorithms is not new—earlier neural architectures such as Neural Turing Machines (NTMs) and differentiable neural computers (DNCs) aimed to render memory and computation differentiable and trainable. Those designs faced brittleness when stacking many differentiable components, which made debugging and generalisation challenging. The current approach seeks to preserve the spirit of those ideas while enabling more reliable deployment by prototyping each component with a clearer, algorithmically informed purpose and by focusing on the blocks that most benefit the execution of specific algorithms. Beyond practical architectures, the discussion hints at richer theoretical frames that inform algorithmic alignment—such as linear algorithmic alignment, causal reasoning, category theory, and the study of asynchronous computation. This evolving theoretical backdrop underscores the interdisciplinary nature of the effort and points to future directions for mathematical understanding of deep learning in algorithmic settings.
Why it matters (impact for developers/enterprises)
For developers, researchers, and enterprises seeking trustworthy AI systems, neural algorithmic reasoning offers a path toward models that reason more like established algorithms. The emphasis on following algorithmic structure can improve reliability and interpretability, two properties critical for production use where failures can be costly. Key practical implications include:
- Improved out-of-distribution generalisation, a crucial property for models deployed in dynamic environments where inputs may differ substantially from the training data.
- Enhanced compositionality, since algorithmic decompositions provide modular building blocks whose solutions can be recombined in principled ways.
- Stronger theoretical grounding for model behaviour, potentially reducing the gap between empirical performance and guaranteed properties typical of classical algorithms. For teams building AI systems that reason about data, graphs, or sequences, the work highlights a disciplined design philosophy: align model architecture and inductive biases with the target algorithm’s structure, rather than rely solely on sheer model capacity. This approach complements data-driven improvements with principled architectural choices inspired by classical computation.
Technical details or Implementation (high-level)
- Decomposition along the lines of classical algorithms: the neural network’s data flow is designed to mirror the update rules and subproblem decomposition of the target algorithm (e.g., Bellman-Ford’s distance updates). When a graph neighbor is considered, a proposal is made, and the best proposal is selected to update the node’s distance.
- Dynamic programming (DP) perspective: many classical computations are expressible as DP problems, and aligning GNNs with DP can improve the network’s ability to learn these procedures.
- Specialized, fine-grained GNNs: the literature shows successful designs for learning to execute a range of algorithms, including linearithmic sequence problems, iterative processes, pointer-based data structures, and persistent auxiliary memory.
- Max aggregation and related architectural choices: the theoretical refinement of algorithmic alignment includes concepts such as linear algorithmic alignment and specific aggregation schemes that support algorithmic execution tasks.
- Broader insights: advancing understanding may require causal reasoning, formal frameworks (like category theory), and considerations of asynchronous computation, all of which inform the design and evaluation of algorithmically aligned models. These details reflect a research program rather than a single recipe, emphasizing careful construction of architectural components and disciplined evaluation to avoid overfitting and to support generalisation to larger inputs.
Key takeaways
- Aligning GNN architectures with the data flow of classical algorithms can improve the learning-to-execute capability of neural models.
- Algorithmic alignment offers benefits for generalisation and sample efficiency, but it must be applied with careful inductive biases to avoid overfitting and poor out-of-distribution performance.
- The approach has yielded specialized GNNs for a variety of algorithmic tasks and connected to broader theoretical concepts like linear algorithmic alignment and causal reasoning.
- Historical work on neural computation (NTMs, DNCs) informs the current approach, while the field continues to refine methods for robust, verifiable execution.
- The overarching goal is to enable AI systems that generalise concepts and procedures reliably, making them more useful for education, decision-making, and complex reasoning tasks.
FAQ
-
What is neural algorithmic reasoning?
It is the study of aligning graph neural networks with classical algorithms to learn to execute computations more reliably and with better generalisation.
-
Why is algorithmic alignment important?
Because alignment with algorithmic structure can improve generalisation and robustness, reducing reliance on superficial data patterns and supporting scalable reasoning.
-
Can GNNs truly execute algorithms?
The evidence suggests that with careful inductive biases and architectural alignment, GNNs can learn to execute certain algorithmic tasks, though not all designs guarantee success across all tasks.
-
What are some notable directions mentioned?
Linear algorithmic alignment, max aggregation, causal reasoning, category theory, and asynchronous computation are highlighted as part of broader theoretical and practical developments.
References
- The Gradient. Neural algorithmic reasoning: aligning GNNs with classical algorithms for reliable generalisation. https://thegradient.pub/neural-algorithmic-reasoning/
More news
Microsoft to turn Foxconn site into Fairwater AI data center, touted as world's most powerful
Microsoft unveils plans for a 1.2 million-square-foot Fairwater AI data center in Wisconsin, housing hundreds of thousands of Nvidia GB200 GPUs. The project promises unprecedented AI training power with a closed-loop cooling system and a cost of $3.3 billion.
Reddit Pushes for Bigger AI Deal with Google: Users and Content in Exchange
Reddit seeks a larger licensing deal with Google, aiming to drive more users and access to Reddit data for AI training, potentially via dynamic pricing and traffic incentives.
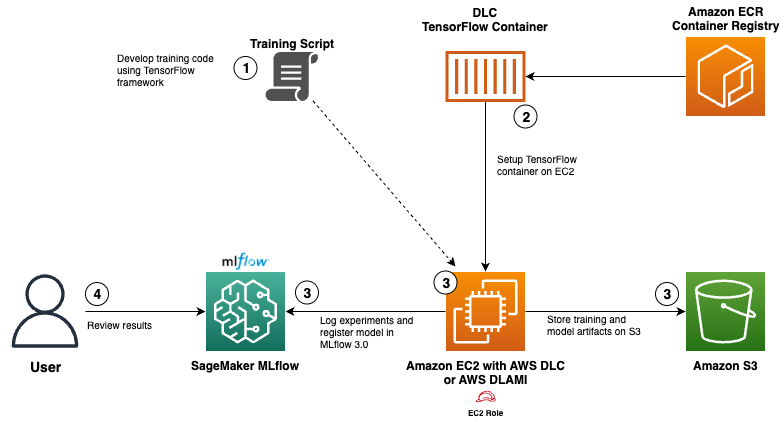
Use AWS Deep Learning Containers with Amazon SageMaker AI managed MLflow
Explore how AWS Deep Learning Containers (DLCs) integrate with SageMaker AI managed MLflow to balance infrastructure control and robust ML governance. A TensorFlow abalone age prediction workflow demonstrates end-to-end tracking, model governance, and deployment traceability.
GPT-5-Codex Addendum: Agentic Coding Optimized GPT-5 with Safety Measures
An addendum detailing GPT-5-Codex, a GPT-5 variant optimized for agentic coding within Codex, with safety mitigations and multi-platform availability.
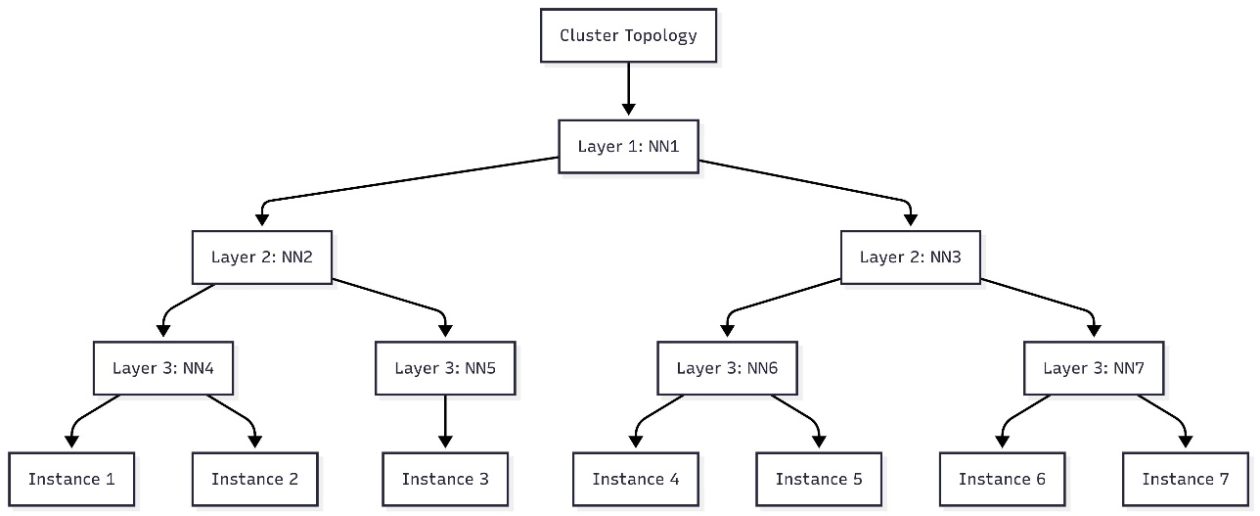
Schedule topology-aware workloads using Amazon SageMaker HyperPod task governance
AWS introduces topology-aware scheduling with SageMaker HyperPod task governance to optimize training efficiency and network latency on EKS clusters, using EC2 topology data to guide job placement.
How Quantization Aware Training Enables Low-Precision Accuracy Recovery
Explores quantization aware training (QAT) and distillation (QAD) as methods to recover accuracy in low-precision models, leveraging NVIDIA's TensorRT Model Optimizer and FP8/NVFP4/MXFP4 formats.